
Zadanie Graf planarny (pla)
Pomóż nam usprawnić bazę zadań!
Graf planarny
Limit pamięci: 512 MB
Dany jest dwuspójny wierzchołkowo\footnote{Graf dwuspójny wierzchołkowo jest to taki graf  , że dla każdego
, że dla każdego  , graf
, graf  jest spójny\footnotemark{}.}\footnotetext{Graf spójny jest to taki graf
jest spójny\footnotemark{}.}\footnotetext{Graf spójny jest to taki graf  , że dla każdego podziału na niepuste podzbiory
, że dla każdego podziału na niepuste podzbiory  istnieje krawędź
istnieje krawędź  , taka że
, taka że  oraz
oraz  .}
graf\footnote{Grafem nazywamy parę
.}
graf\footnote{Grafem nazywamy parę 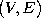 , gdzie
, gdzie  jest multizbiorem\footnotemark{} dwuelementowych podzbiorów
jest multizbiorem\footnotemark{} dwuelementowych podzbiorów  .}\footnotetext{Multizbiór to zbiór, w którym elementy mogą się powtarzać; formalnie, jest to funkcja z dowolnego zbioru w zbiór liczb naturalnych.} planarny\footnote{Graf
.}\footnotetext{Multizbiór to zbiór, w którym elementy mogą się powtarzać; formalnie, jest to funkcja z dowolnego zbioru w zbiór liczb naturalnych.} planarny\footnote{Graf  nazywamy planarnym, gdy istnieje planarne włożenie\footnotemark{} tego grafu w płaszczyznę.}\footnotetext{Planarne włożenie grafu planarnego w płaszczyznę to taki rysunek grafu, na którym każdemu wierzchołkowi przyporządkowany jest inny punkt płaszczyzny, natomiast każdej krawędzi - krzywa łącząca punkty przyporządkowane wierzchołkom połączonym przez tę krawędź.
Każda krzywa może przecinać się z innym wierzchołkiem lub krzywą jedynie w swoim końcu.}
nazywamy planarnym, gdy istnieje planarne włożenie\footnotemark{} tego grafu w płaszczyznę.}\footnotetext{Planarne włożenie grafu planarnego w płaszczyznę to taki rysunek grafu, na którym każdemu wierzchołkowi przyporządkowany jest inny punkt płaszczyzny, natomiast każdej krawędzi - krzywa łącząca punkty przyporządkowane wierzchołkom połączonym przez tę krawędź.
Każda krzywa może przecinać się z innym wierzchołkiem lub krzywą jedynie w swoim końcu.}  .
W tym grafie co najwyżej dwie ściany\footnote{Rozważmy planarne włożenie grafu planarnego w płaszczyznę. Ścianą grafu nazywamy każdy z obszarów płaszczyzny ograniczony krzywymi odpowiadającymi krawędziom. Zwróć uwagę, że w każdym grafie istnieje również nieskończona ściana "otaczająca" graf.} są otoczone nieparzystą liczbą krawędzi.
Dane jest również planarne włożenie grafu
.
W tym grafie co najwyżej dwie ściany\footnote{Rozważmy planarne włożenie grafu planarnego w płaszczyznę. Ścianą grafu nazywamy każdy z obszarów płaszczyzny ograniczony krzywymi odpowiadającymi krawędziom. Zwróć uwagę, że w każdym grafie istnieje również nieskończona ściana "otaczająca" graf.} są otoczone nieparzystą liczbą krawędzi.
Dane jest również planarne włożenie grafu  w płaszczyznę.
Należy sprawdzić, czy istnieje podział krawędzi
w płaszczyznę.
Należy sprawdzić, czy istnieje podział krawędzi 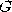 na pewną liczbę cykli prostych\footnote{Zbiór krawędzi
na pewną liczbę cykli prostych\footnote{Zbiór krawędzi 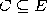 nazywamy cyklem prostym, gdy krawędzie te tworzą graf spójny, w którym każdy wierzchołek jest incydentny z dokładnie dwiema krawędziami.} parzystej długości.
nazywamy cyklem prostym, gdy krawędzie te tworzą graf spójny, w którym każdy wierzchołek jest incydentny z dokładnie dwiema krawędziami.} parzystej długości.
Wejście
W pierwszym wierszu wejścia znajdują się dwie liczby całkowite  i
i  (
( ,
,  ).
Liczba
).
Liczba  oznacza liczbę wierzchołków, zaś
oznacza liczbę wierzchołków, zaś  - liczbę krawędzi w grafie
- liczbę krawędzi w grafie  .
Wierzchołki są ponumerowane liczbami od
.
Wierzchołki są ponumerowane liczbami od  do
do  , zaś krawędzie - liczbami od
, zaś krawędzie - liczbami od  do
do  .
Każda z krawędzi łączy dwa różne wierzchołki.
Pomiędzy daną parą wierzchołków może istnieć wiele krawędzi.
.
Każda z krawędzi łączy dwa różne wierzchołki.
Pomiędzy daną parą wierzchołków może istnieć wiele krawędzi.
Dalej następuje  wierszy opisujących krawędzie grafu;
wierszy opisujących krawędzie grafu;  -ty z tych wierszy zawiera opis krawędzi incydentnych z wierzchołkiem
-ty z tych wierszy zawiera opis krawędzi incydentnych z wierzchołkiem  .
Opis ten rozpoczyna się liczbą całkowitą
.
Opis ten rozpoczyna się liczbą całkowitą 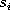 (
( ), po której następuje lista
), po której następuje lista  liczb całkowitych z zakresu od
liczb całkowitych z zakresu od 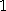 do
do 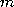 .
Każda z tych liczb oznacza numer jednej krawędzi incydentnej z wierzchołkiem
.
Każda z tych liczb oznacza numer jednej krawędzi incydentnej z wierzchołkiem  .
Lista zawiera krawędzie uporządkowane kolejno wokół wierzchołka
.
Lista zawiera krawędzie uporządkowane kolejno wokół wierzchołka  , w porządku zgodnym z kierunkiem ruchu wskazówek zegara.
, w porządku zgodnym z kierunkiem ruchu wskazówek zegara.
Wyjście
Jeśli odpowiedni podział krawędzi nie istnieje, to w jedynym wierszu wyjścia należy wypisać słowo NIE.
W przeciwnym razie, w pierwszym wierszu wyjścia należy wypisać słowo TAK.
W kolejnych wierszach należy wypisać poprawny podział krawędzi grafu  na cykle proste.
Każdy z tych wierszy powinien rozpoczynać się liczbą całkowitą
na cykle proste.
Każdy z tych wierszy powinien rozpoczynać się liczbą całkowitą  (
( ).
Po niej wypisać należy
).
Po niej wypisać należy  numerów krawędzi tworzących opisywany cykl prosty.
Każde dwie kolejne krawędzie powinny mieć wspólny wierzchołek.
Każda krawędź powinna zostać wypisana na wyjściu dokładnie raz.
numerów krawędzi tworzących opisywany cykl prosty.
Każde dwie kolejne krawędzie powinny mieć wspólny wierzchołek.
Każda krawędź powinna zostać wypisana na wyjściu dokładnie raz.
Przykład
Dla danych wejściowych:
10 16 2 1 8 2 8 7 4 1 9 2 14 4 6 13 7 14 4 16 10 9 15 4 16 15 13 12 4 2 10 3 11 4 5 12 6 11 2 3 4 2 4 5
poprawną odpowiedzią jest:
TAK 6 16 10 3 4 5 12 4 6 11 2 14 6 8 1 9 15 13 7
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English